La conversion industrielle totale de la chaleur en travail

L’exposé du moteur thermique périodique pendulaire et différentiel de rendements théorique

Tous les moteurs thermodynamiques connus dans le monde comportent une admission de gaz, une détente et un échappement. Leur production est définie par l’équivalence de Joule entre chaleur et travail : Q (calories converties) = W (travail produit), et leur rendement théorique est défini par le second principe des rendements théoriques thermodynamiques de Carnot, que nous pouvons présenter sous la forme (T1 – T2)/T1 : T1 représentant la température initiale du cycle et T2 sa température finale.

Le nouveau cycle ici décrit plus bas, intercale un pendule thermodynamique dans le cycle de détente d’un gaz … Voir figure 1. Ce pendule est obtenu par exemple en connectant le piston d’un moteur thermique conventionnel (1) à un volant d’inertie libre (2) et à les mettre tous deux en opposition permanente dans une enceinte cylindrique (3) au moyen d’un câble de liaison. Une partie de ce câble (4) est enroulée étroitement autour de l’axe de rotation du volant d’inertie (5), et la partie libre du câble, interposée entre les deux restes tout le temps étroitement tendue entre les deux. Le montage est facile à comprendre.

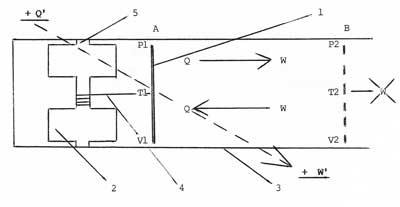
Figure 1

En théorie un volant d’inertie mobilisé restitue toute l’énergie cinétique qui lui a été communiquée. Soit un travail rotatif W. Ce travail est produit par la détente des gaz contenus dans l’enceinte, conformément aux deux premiers principes de thermodynamique. Donc de rendement théorique de Carnot : (T1 – T2) / T1, qui nous indiffère. Entre le début et la fin de la détente des gaz, c’est-à-dire entre le point A et le point B de la figure 1, par exemple, le mouvement du piston consomme Q calories et produit W travail pour mobiliser son volant. Ce faisant, la température des gaz évolue entre T1 initiale et T2, finale plus petite que T1, et leur pression entre P1 initiale et P2 finale plus petit que P1, dans le volume initial V1 et le volume final V2 plus grand que V1. Une fois tout le câble de liaison interposé entre le piston et le volant tendu en totalité, le câble de liaison (4) jusqu’alors enroulé autour de l’axe de rotation (5) du volant d’inertie (2), passe d’un bord à l’autre de l’axe de rotation du volant. En effet, du fait que le volant lancé continue de tourner (figure 2), le câble (4) vient s’enrouler autour de l’axe de rotation (5), en sens inverse du sens précédent. Le volant d’inertie mobilisé sert donc de rappel au piston en renversant son mouvement et en théorie le ramène à son point de départ en restituant dans l’enceinte la température initiale, la pression initiale dans le volume initial.

Figure 2

De A jusqu’à B, c’est le piston qui entraîne le volant d’inertie. Une fois en B, le piston marque une courte pause et d’actif devient passif dés lors qu’il est entraîné par le volant d’inertie qui continue de tourner et renverse son mouvement. Une fois revenu en A, Le volant et le piston marquent tous deux une courte pause et les gaz de l’enceinte recomprimés sont portés en théorie à leur pression initiale, à leur température initiale, dans le volume initial et agissent sur le piston.  Le volant et le piston renversent dons tous deux leur mouvement respectif (linéaire et circulaire) et initient un nouveau cycle, en principe identique au précédent … En somme, un mouvement d’horlogerie, mais un mouvement d’horlogerie de puissance.

Bien entendu ceci est une vue de l’esprit et dans la pratique les forces de résistance amortissant le mouvement finiront par l’arrêter. Mais il est parfaitement possible dans la réalité cette fois-ci de rendre perpétuel un mouvement amorti en l’entretenant de petites poussées de compensation (ce qui explique que le rendement final vrai ne sera jamais de 100 %, car une machine parfaite est inconcevable) … Mais certains dispositifs annexes plus sophistiqués sur lesquels je m’étends pas et qui sont suggérés dans le brevet peuvent permettre d’accéder concrètement à ce résultat vrai. En résumé, dans un sens, par exemple de A jusqu’à B (voir schéma 1), c’est le volant d’inertie qui sert passif et entraîné par le piston poussé par les gaz sous pression, et dans le sens contraire, de B jusqu’à A, le volant jusqu’alors passif entre en action,  et tire le piston en sens inverse. Il sert de rappel, de balancier au piston et le ramène en théorie à son point de départ en A tout en recomprimant les gaz détendus entre A et B. Ce faisant, il rétablit toujours en théorie les volumes, pressions et températures à leurs valeurs initiales, ce qui idéalement permet de recommencer un cycle identique au précédent.

Un tel ensemble est par définition adiabatique, puisqu’il ne produit et ne consomme rien en dehors de lui-même, ce qui est la définition même de tout ensemble adiabatique, quel qu’il soit. En effet, une fois le dispositif revenu à sa configuration première, la pression rétablie renverse à nouveau le mouvement du piston qui repart pour un nouveau cycle, alors que le volant après une courte pause repart lui aussi en sens rotatoire inverse … et ce mouvement en théorie devient perpétuel. Il est assimilable à une onde stationnaire, avec une oscillation linéaire pour le piston et rotatoire qui change de sens à chaque cycle successif pour le volant d’inertie. Les deux figures 1 et 2 permettent de comprendre la logique de ce dispositif. Son entropie est constante en théorie. Il ne procède en théorie à aucun échange avec le milieu extérieur à lui-même.

Néanmoins en dedans de ce dispositif adiabatique et isentropique nous enregistrons des variations cycliques de températures, de pressions et de volumes. En particulier les températures évoluent de façon périodique entre T1 – T2 – T1 – T2 … etc., en théorie perpétuellement.

Nous allons commencer notre cycle en surchargeant en calories l’enceinte de révolution des gaz. Nous obtenons cette surcharge en portant les gaz de la température initiale T1 à la température T3 = T1 + (T1 – T2).

Le brevet explique comment obtenir industriellement cette surcharge thermique dans la pratique afin d’obtenir un cycle industriel.

J’invoque ici la loi de Charles :

Dans cette enceinte fermée remplie de gaz, la variation de températures des gaz est une fonction de leur variation de pressions. Si nous élevons la pression la température s’élève, et si nous l’abaissons la température s’abaisse. Cette loi bien connue en physique n’est contestée par personne.

Nous sommes donc en droit d’écrire :

(delta P) = f x (delta T)
(loi générale)
• (delta T) étant la variation de températures
• Et (delta P) la variation de pressions.

Si :

T3 = T1 + (T1 – T2)
(T3 – T1) = (T1 – T2)
Soit delta T’ la variation (T3 – T1), obtenue entre T3 et T1, et delta T la variation (T1 – T2), entre T1 et T2.

Si (delta T’) = (delta T)

f x (delta T’) = f x (delta T) :

Si (delta P’) est obtenu entre T3 et T1 et (delta P) entre T1 et T2 :

(delta P’) = (delta P)

Par conséquent le travail disponible W’ obtenu entre T3 et T1 devient exactement égal à celui W, obtenu entre T1 et T2.

Le travail W va servir à mobiliser le volant d’inertie dans un échange perpétuel W/Q/W/Q/W … etc., comme dans le dispositif non surchargé en chaleur en situation adiabatique, et le supplément de  travail W’ obtenu par la surchauffe (T3 – T1) devient intégralement disponible en dehors du dispositif. Il est produit spontanément par équipartage de forces produites sur les deux faces du volant : l’une intérieure va servir à entretenir le mouvement du dispositif et l’autre, extérieure, est disponible en dehors du dispositif. Si nous prélevons ce travail en dehors du dispositif, celui-ci, bien que n’étant plus adiabatique, se comporte comme s’il l’était … en effet :

La première production est obtenue en équivalence de Joule Q = W

La deuxième l’est aussi. Si Q est la valeur calorique convertie, produite entre T3 et T1 et si elle est équivalente à celle servant à l’entretien du mouvement entre T1 et T2 : Du fait que nous soustrayons W’ en totalité … Nous soustrayons du même coup Q’ en totalité et le pendule thermodynamique adiabatique auquel nous ajoutons et soustrayons une quantité calorique exactement équivalente demeure comme adiabatique … en dépit qu’il soit traversé par un flux de chaleur qui entre sous forme de chaleur et en ressort sous forme de travail exclusivement. Nous n’avons plus besoin d’évacuer de calorique (la source froide), ni de gaz à chaque cycle consécutif. Les pertes théoriques sont nulles.

Le rendement théorique de cette dernière conversion … est un.

C.Q.F.D.

Contrairement à un dispositif classique qui essaye de convertir la plus grande partie d’une réserve calorique donné, ici nous ne cherchons à convertir qu’une surcharge thermique … Et ceci, dans les conditions décrites, peut être produit en équivalence de Joule. Le cycle du pendule est inchangé, ce qui permet de produire des conversions seulement subordonnées dans le temps au rythme du cycle pendulaire, dont nous sommes à même de commander tous les paramètres. Le problème de l’injection industrielle rapide de chaleur à partir d’une température donnée, est résolu dans les suggestions du brevet. Il peut s’appliquer à n’importe quelle température sans difficultés.

Le dispositif expérimental de vérification vérifie bien cette équivalence. Ses gaz ne sortent jamais de leur enceinte hermétiquement fermée et bien qu’à chaque cycle on procède à une surchauffe … Il ne chauffe jamais d’un cycle à l’autre. L’équivalence de Joule est vérifiée … aux erreurs de manipulation près, qui sont de l’ordre de deux à trois pour cent de pertes dans le dispositif construit … ce qui de toute façon serait inconcevable avec un dispositif classique.

La puissance du dispositif n’a pas de limites théoriques. Ses limites sont celles de la source de chaleur mise à disposition. Son calibre détermine sa puissance … sans limites non plus. La température à traiter nous indiffère … Bien entendu plus la température tendra vers zéro et plus la puissance disponible sera faible, et vice versa (loi de Neernst : l’entropie d’un système tend vers zéro quand sa température tend vers zéro).

Si nous dépassons les limites d’interconversion du pendule construit, pour la surcharge supplémentaire nous retombons dans les considérations du deuxième principe de thermodynamique pour le supplément … Et cycle après cycle la dégradation du mouvement finira par l’arrêter … Rien ne nous y oblige. Si au contraire nous restons en dessous des limites de conversions thermodynamique du pendule, le dispositif ne sera pas exploité dans toute sa capacité, ce qui ne change rien au processus. Bien entendu, des régulations sont possibles pour éviter un emballement ou bien un arrêt du processus.

N° de demande du brevet international : WO 2009/112666 A2

Auteur : Dr Albert COHEN

Pour prendre contact avec l’inventeur : Dr Albert COHEN

2 rue Bonnet – 92100 Clichy – France

Tél. : + 33 1 47 39 69 43